Problem Transformation¶

The skml.problem_transformation module implements so called meta-estimators to solve multi-label classification problems by transforming them into a number of easier problems, i.e. binary classification problems.

Binary Relevance¶

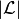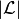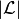Binary Relevance (skml.problem_transformation.BinaryRelevance) transforms a problem of multi-classification with $|\mathcal{L}|$ labels into a problem of $|\mathcal{L}|$ binary classification problems, hence trains $|\mathcal{L}|$ classifiers that decide label-wise, if the example that is currently being observed should have the label or not. (Dubbed PT-4 in the cited paper.)

Note, that binary relevance is not capable of modeling label interdependence.

References:

[1]	“Multi-Label Classification: An Overview.” Tsoumakas, Grigorios and Ioannis Katakis. in IJDWM 3 (2007): 1-13.

Label Powerset¶

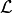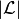Label Powerset (skml.problem_transformation.LabelPowerset) transforms a multi-class classification problem into one multi-class problem, where all possible label combinations are used as classes. So each possible combination of labels is turned into one class. If the underlying multi-label problem operates on the label space $\mathcal{L}$ with $|\mathcal{L}|$ labels, label powerset will train 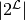$|2^{\mathcal{L}}|$ classifiers, where each one decides if the label combination should be assigned to an example.

Note, that while label powerset can model label interdependence, the computational feasibility can be reduced for a large number of labels, as the number of trained classifiers grows exponentially. (Dubbed PT-5 in the cited paper.)

References:

[1]	“Multi-Label Classification: An Overview.” Tsoumakas, Grigorios and Ioannis Katakis. in IJDWM 3 (2007): 1-13.

Classifier Chains¶

Classifier chains (skml.problem_transformation.ClassifierChain) improve the binary relevance (skml.problem_transformation.BinaryRelevance) method to use label interdependence as well. For each label a classifier is trained. Besides the first classifier in the chain, each subsequent classifier is trained on a modified input vector, where the previous predicted labels are incorporated. Thus, a chain of classifiers is predicted, and each classifier in the chain gets also the previous class predictions as an input.

Note, that the performance of a single chain depends heavily on the order of the classifiers in the chain.

References:

[2]	“Classifier chains for multi-label classification”, Read, J., Pfahringer, B., Holmes, G. & Frank, E. (2009). In Proceedings of European conference on Machine Learning and Knowledge Discovery in Databases 2009 (ECML PKDD 2009), Part II, LNAI 5782(pp. 254-269). Berlin: Springer.

Probabilistic Classifier Chains¶

Probabilistic Classifier Chains (skml.problem_transformation.ProbabilisticClassifierChain) –also known as PCC– are an extension to the classic Classifier Chains (skml.problem_transformation.ClassifierChain) and can be seen as a discrete greedy approximation of probabilistic classifier chains with probabilities valued zero/one [3].

For each label a classifier is trained as in CC, however probabilistic classifiers are used. In fact [3], when used with non-probabilistic classifiers, CC is recovered from the posterior probability distribution 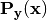$\mathbf{P}_\mathbf{y}(\mathbf{x})$ .

Note, that PCC performs best, when a loss function that models label interdendence (such as Subset 0/1 loss) is used, and the labels in the data set are in fact interdependent. For more information on this, see [3].

The training is equivalent to CC, the inference (prediction) however is more complex. For a detailed description of the inference, see skml.problem_transformation.ProbabilisticClassifierChains directly, have a look at the source code, or refer to the paper [3].

References:

[3]	“Bayes Optimal Multilabel Classification via Probabilistic Classifier Chains”, K. Dembczynski, W. Cheng, E. Hüllermeier (2010). ICML 2010